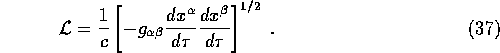
To find the motion of planets and light rays in a Schwartzschild spacetime we must first find the geodesic equations. This is best done by working from the Lagrangian
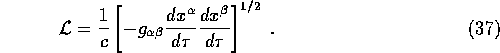
Assuming that the orbits remain permanently in the equatorial plane [ as in
Newtonian theory ] i.e. 
, the Lagrangian is:
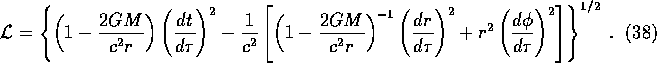
The Euler- Lagrange equations are
Now
so
This is just energy conservation. Also
so
This is conservation of angular momentum.
Remember that 
with 
for timelike orbits and
for null orbits, so
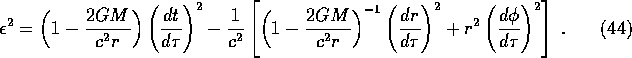
We have
Substituting these into the above, we get
This is the Newtonian energy equation with a modification to the 
term. Using 
and putting 
we get
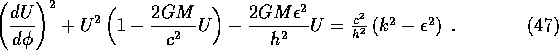
This equation can in fact be integrated immediately, but it leads to elliptical integrals, which are awkward to handle. We therefor differentiate to obtain the equation:
For timelike orbits [ ] this is just Newton's equation
apart from the last term.